√100以上 なぞなぞ 小学 2 年生 305282

３年生からのなぞなぞ 謎のなぞなぞシリーズ第３弾 南山大学附属小学校

なぞなぞ 小学 2 年生

なぞなぞ 小学 2 年生-

教えてもらう前と後 小学生が考えた なぞなぞ問題 ４問 ページ 2 Aznews アズニュース

プリント 子供向けなぞなぞ100問のプリント

なぞなぞブック 気が重いよ 伊那篇

旧版 考える力がつく算数脳パズル なぞぺ 3 5歳 小学3年生 Chuohネットショップ

クイズ この絵 なんて読む 江戸時代の脳トレ はんじ絵 富裕層向け資産防衛メディア 幻冬舎ゴールドオンライン

子供が言葉を増やす最高の遊び クロスワード なぞなぞ しりとり オススメリスト 子育ての本をたくさん読む ブログ

なぞなぞクイズ 子供向け3 小学校低学年 Youtube

なぞなぞ で子供の頭がよくなる レベル別おもしろなぞなぞ集 りんごちゃんのおけいこラボ 学研の幼児ワーク

小学生クイズ 面白いなぞなぞ問題 低学年向け 問 生き物編 キニナル情報 コレから

わかるかな なぞなぞ小学1 2年生 なぞなぞたんけん隊 武士 寺山 本 通販 Amazon

いろはのなぞなぞなぞなぞ大冒険 こども 子供 小学生 クイズ バーゲンブック バーゲン本 バーゲンブックストアb Books 通販 Yahoo ショッピング

わかるかな なぞなぞ小学1 2年生 なぞなぞたんけん隊 武士 寺山 本 通販 Amazon

4歳女の子 なぞなぞ がマイブーム 夫と娘と猫との暮らし

なぞなぞ 小学校低学年向け 簡単で面白い問題 ひらめきと遊びの時間

小学２年生 漢字クイズ 問題プリント ちびむすドリル 小学生

ボード なぞなぞ のピン

小学２年生 漢字クイズ 問題プリント ちびむすドリル 小学生

なぞなぞ低学年向け30選 小学生におすすめ簡単ひらがな問題大特集 子供と一緒に楽しく遊べる手作りおもちゃ

高学年向け 小学校でできる 小学生のためのおもしろいなぞなぞ問題集 なぞなぞ ん

小学生対象 校舎対抗なぞなぞ大会のご案内 富山育英センター

なぞなぞ 小学生 子供向けのなぞなぞ500問以上 なぞなぞ王国

難問なぞなぞ 意外と難しいなぞなぞ 15問 クイズどうでしょう

なぞなぞアドベンチャー 小学1年生 2年生 ゆうき やすたか ふじもと かずや 本 通販 Amazon

あそぼ かっこいい なぞなぞ １ ２年生の通販 大林 のぼる 嵩瀬 ひろし 紙の本 Honto本の通販ストア

小学生向け 低学年から楽しめる かんたん なぞなぞ 25問

小学生 謎解き問題を無料でプリントできるサイト４選 Studywith 親子の学びブログ

小学校なぞなぞ その1 これなーんだ 保育や子育てが広がる 遊び と 学び のプラットフォーム ほいくる

楽天ブックス わくわくなぞなぞランド 小学1 2年生 本間正夫 本

藍那小学校 児童 登美丘西小学校 校長先生 なぞなぞ問題 3問 藍那小 登美丘西小 なぞなぞ校長の教育法 教えてもらう前と後 ページ 4 Aznews アズニュース

小学生向けのクイズ

簡単で面白いクイズ なぞなぞ問題 子供向け 幼稚園児から小学生にピッタリ 気になるネタが大集合

ドラえもんのなぞなぞブック 小学二年生平成1年1月号付録 案と絵 ヨシダ忠 伊東古本店 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋

教えてもらう前と後 小学生が考えた なぞなぞ問題 ４問 ページ 2 Aznews アズニュース

いろはのなぞなぞなぞなぞ大冒険 こども 子供 小学生 クイズ バーゲンブック バーゲン本 バーゲンブックストアb Books 通販 Yahoo ショッピング

例題 クイズ あなたは小学5年生より賢いの 日本テレビ

小学生向け論理クイズ 超簡単 頭の体操に良い問題 全15問

簡単で面白いクイズ なぞなぞ問題 子供向け 幼稚園児から小学生にピッタリ 気になるネタが大集合

106 ばっちりくんドリル クイズ なぞなぞ 応用編 小学校受験 合格対策問題集 教材の 理英会出版

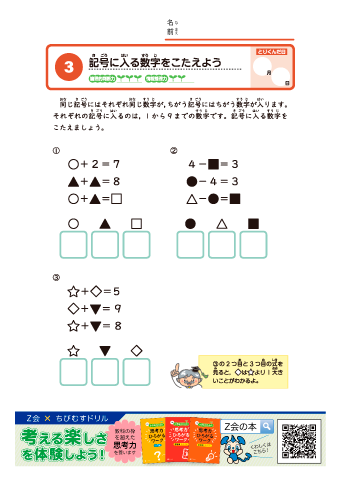
なぞなぞ 問題 小学生 小学生 謎解き問題を無料でプリントできるサイト４選

ひらめき力upに効果大 小学生がグングン伸びる知能訓練とは 5分で読める 教えてもらう前と後 Mbsコラム

藍那小学校 児童 登美丘西小学校 校長先生 なぞなぞ問題 3問 藍那小 登美丘西小 なぞなぞ校長の教育法 教えてもらう前と後 ページ 4 Aznews アズニュース

なぞなぞ本 かるた23選 幼稚園児から小学生まで人気なのは Cozre コズレ 子育てマガジン

50 なぞなぞ 小学生 低学年 プリント 最高のぬりえ

子どもと一緒に頭の体操 簡単おもしろダジャレなぞなぞ集 りんごちゃんのおけいこラボ 学研の幼児ワーク

アメリカの小学1年生 出題されたなぞなぞに対し哲学的な答えを返す ライブドアニュース

みんなでたのしい なぞなぞ小学1 2年生 嵩瀬 ひろし 黒崎玄 本 通販 Amazon

簡単で面白いクイズ なぞなぞ動物問題 幼稚園児や子どもたちにピッタリ 気になるネタが大集合

なぞなぞ で子供の頭がよくなる レベル別おもしろなぞなぞ集 りんごちゃんのおけいこラボ 学研の幼児ワーク

低学年向け 小学校でできる 小学生のためのおもしろいなぞなぞ問題集 なぞなぞ ん

50 なぞなぞ 小学生 低学年 プリント 最高のぬりえ

なぞなぞ本 かるた23選 幼稚園児から小学生まで人気なのは Cozre コズレ 子育てマガジン

昭和レトロ 小学館 付録 なぞなぞじてん クイズじてん なぞなぞブック ドラえもん 小学三年生 小学二年生 の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版

昭和50年代のなぞなぞ本のなぞなぞがすごい デジタルリマスター版 デイリーポータルz

累計50万部の人気シリーズに語彙力が登場 丸暗記 漢字書き取り じゃない画期的な一冊 かんき出版のプレスリリース

なぞなぞ本 問題集 小学生に人気のおすすめ11選 こそだてハック

小学生 クロスワードパズルを無料でプリントできるサイト３選 Studywith 親子の学びブログ

なぞなぞ 小学生向け のアイデア 13 件 なぞなぞ クイズ 問題 クイズ 雑学

年長 １年生 新入学 新学期 友だちと楽しもう 学校なぞなぞ集 簡単 ちょっと難しい 漢字の問題もあるよ りんごちゃんのおけいこラボ 学研の幼児ワーク

ひっかけクイズ問題 簡単で子供も面白い 大人も小学生も盛り上がる 動物ネタもあり クイズっす

いろはのなぞなぞ漢字 数字なぞなぞ こども クイズ 小学生 クイズ 小学生 バーゲンブック バーゲン本 バーゲンブックストアb Books 通販 Yahoo ショッピング

思考力 発想力を磨く 佐賀県武内小学校 謎解き なぞぺー問題4問 佐藤健 全問正解 謎ペーなぞなぞ4問 教えてもらう前と後 ページ 5 Aznews アズニュース

遊びながら覚える 都道府県なぞなぞ レベルふつう 都道府県らくがき

子どもと一緒に頭の体操 簡単おもしろダジャレなぞなぞ集 りんごちゃんのおけいこラボ 学研の幼児ワーク

小学館 昭和48 49年 小学舘 1 2年生 付録 なぞなぞじてんの通販 By Green ショウガクカンならラクマ

ミラクルかわいい なぞなぞ１ ２年生 ナツメ社

ピカピカの1年生向けの楽しい簡単小学生なぞなぞ問題集 なぞなぞ ん

なぞなぞ ポポちゃん 小学二年生昭和40年11月号付録 山根あおおに 絵 木の実和 案 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋

プリント 子供向けなぞなぞ100問のプリント

雑誌 小学二年生 付録本 なぞなぞブック なぜなに怪獣ブック ノスタルジック ヒーローズ

なぞなぞ２年３年生大百科 650問 リドル なぞ田 本 通販 Amazon

うんこドリルから 日本一うんこが出てくるなぞなぞ 3 12発売 リセマム

小学館 昭和48 49年 小学舘 1 2年生 付録 なぞなぞじてんの通販 By Green ショウガクカンならラクマ

30年ぐらい前のなぞなぞ本のなぞなぞがすごい デイリーポータルz

なぞなぞクイズ 子供向け２ 小学校低学年 Youtube

考える力がつく算数脳パズル なぞぺ 2 5歳 小学3年生 Chuohネットショップ

なぞなぞ 問題 小学生 小学生 謎解き問題を無料でプリントできるサイト４選

子供が言葉を増やす最高の遊び クロスワード なぞなぞ しりとり オススメリスト 子育ての本をたくさん読む ブログ

３年生からのなぞなぞ 謎のなぞなぞシリーズ第３弾 南山大学附属小学校

昭和46年7月小学2年生 ふろく きせかえ なぞなぞ本 オバq 谷ゆきこ 逸見じゅんこ 表紙 昭和レトロ 藤子不二雄 我孫子 素雄 の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版

プリント 初級なぞなぞ260問のプリント

ドラえもんのなぞなぞブック 小学二年生平成1年1月号付録 案と絵 ヨシダ忠 伊東古本店 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋

子供向け とっても楽しい ワクワクなぞなぞクイズ Youtube なぞなぞ クイズ 子供向け

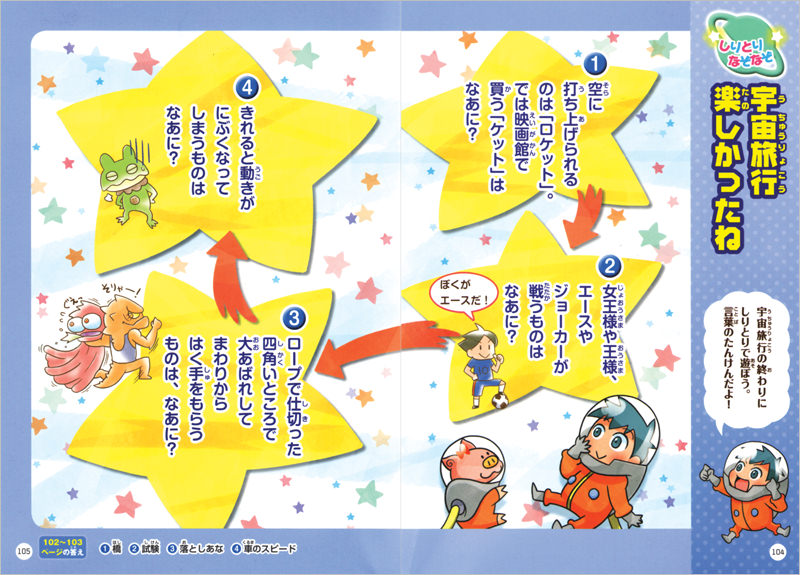
たのしくあそぼう なぞなぞ３ ４年生 高橋書店

モンスターたちとなぞなぞで対決 ドラゴンクエスト の世界が舞台のなぞなぞブックが8月2日 金 発売 ドラクエ パラダイス ドラパラ ドラゴンクエスト公式サイト Square Enix

楽天ブックス ちびまる子ちゃんのなぞなぞ 2年生 さくらももこ 本

答え 解説あり 何問解ける 小学生でも解ける謎解き0問 その1 なぞまっぷ 日本最大のリアル脱出ゲーム 謎解き情報サイト

驚くばかりなぞなぞ 問題 子供 向け かわいい子供たちの画像

幼児の簡単なぞなぞ１００集 文字のみプリント 幼児教材 知育プリント ちびむすドリル 幼児の学習素材館

2 年生 なぞなぞ シモネタ

いろはのなぞなぞ漢字 数字なぞなぞ こども クイズ 小学生 クイズ 小学生 バーゲンブック バーゲン本 バーゲンブックストアb Books 通販 Yahoo ショッピング

ひっかけなぞなぞ 全15問 解けたら異常 8割の人は解けないイジワル問題 Youtube

小学館 昭和48 49年 小学舘 1 2年生 付録 なぞなぞじてんの通販 By Green ショウガクカンならラクマ

ひらめき力upに効果大 小学生がグングン伸びる知能訓練とは 5分で読める 教えてもらう前と後 Mbsコラム

たのしくことばが身につく なぞなぞ１０００ 高橋 啓恵 著 深谷 圭助 監修 紀伊國屋書店ウェブストア オンライン書店 本 雑誌の通販 電子書籍ストア

ドラえもんのなぞなぞブック 小学二年生平成1年1月号付録 案と絵 ヨシダ忠 伊東古本店 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋

幼児なぞなぞ１００集 カードゲーム ミニ絵本 幼児教材 知育プリント ちびむすドリル 幼児の学習素材館

昭和43年 小学2年生8月号付録 のろいのねこ なぞなぞまんが いじわるまんが レトロ スタイル

最高の低 学年 なぞなぞ 最高のぬりえ

なぞなぞ 簡単でしたかー 答えは全て小学1年生で習う漢字でした 漢字 かんじもん Kanjimon の漫画

小学 低 学年 なぞなぞ ニスヌーピー 壁紙